lmds: Landmark Multi-Dimensional Scaling
A fast dimensionality reduction method scaleable to large numbers of samples.
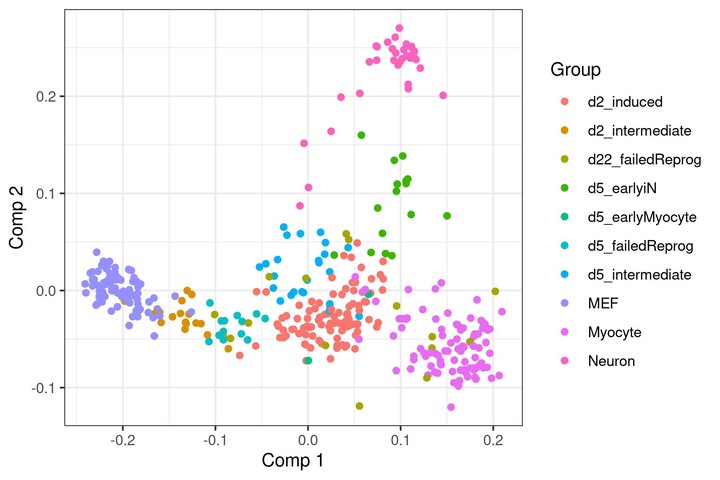 A dimensionality reduction obtained by lmds.
A dimensionality reduction obtained by lmds.Multi-dimensional scaling (MDS) (Kruskal 1964) is a dimensionality reduction method used for visualising and denoising high-dimensional data. However, since MDS requires calculating the distances between all pairs of data points, it does not scale well to datasets with a large number of samples.
We released lmds v0.1.0, an implementation of Landmark MDS (LMDS) (de Silva and Tenenbaum 2004). Landmark MDS only calculates the distances between a set of landmarks and all other data points, thereby sacrificing determinism for scalability.
Regular MDS
A single-cell transcriptomics dataset (Treutlein et al. 2016) is used to demonstrate (L)MDS, containing 392 profiles which measure the abundance levels of 2000 different molecules within individual cells. Note that while the dataset is thus only a 392×2000 matrix, LMDS is designed to scale to much higher dimensionality, as demonstrated in the last section.
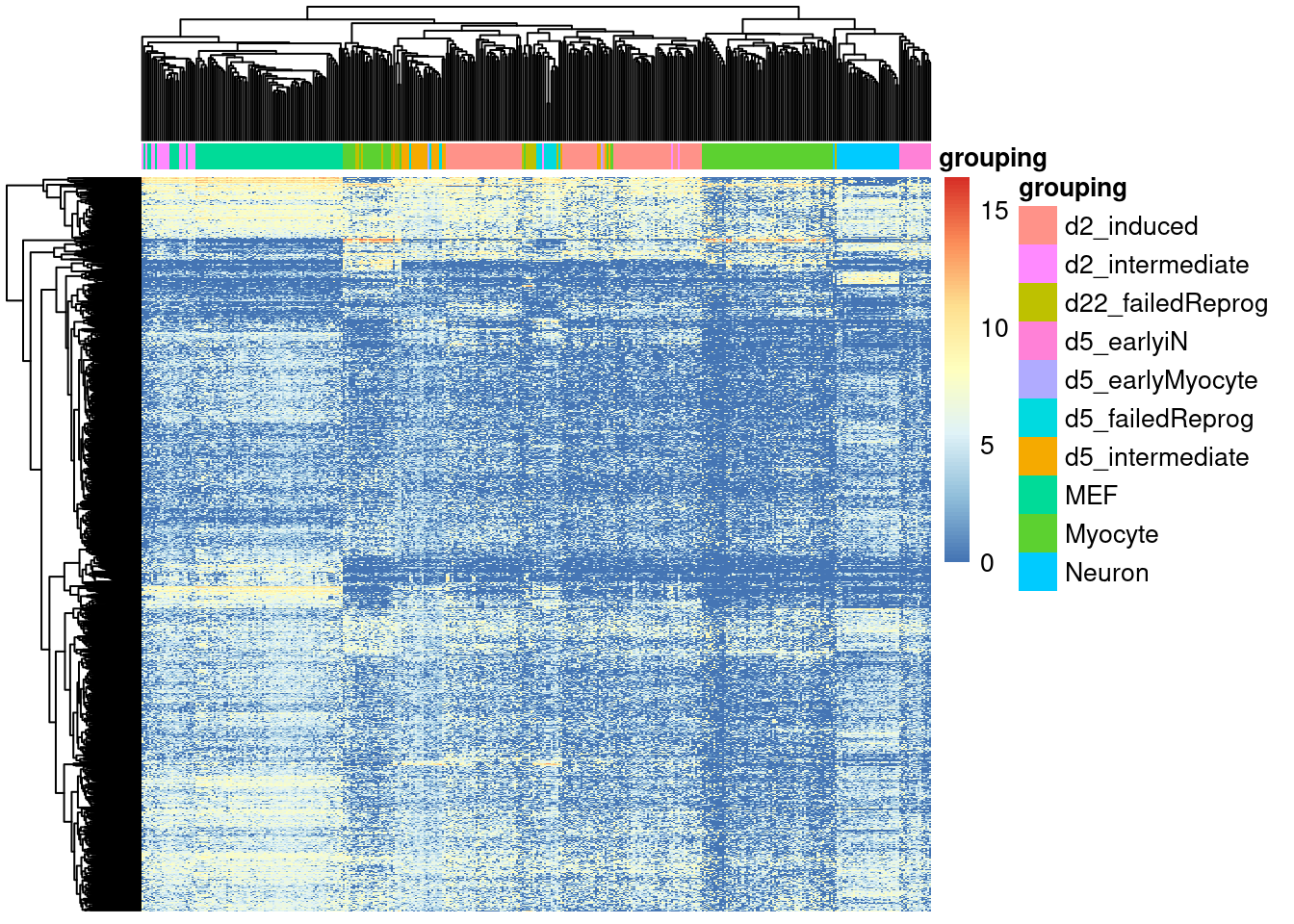
Simply looking at the raw expression values as a heatmap reveals little to no information:
library(tidyverse)
set.seed(1)
dataset <- dyno::fibroblast_reprogramming_treutlein
cell_info <- data.frame(grouping = dataset$grouping)
pheatmap::pheatmap(
t(as.matrix(dataset$expression)),
show_colnames = FALSE,
show_rownames = FALSE,
annotation_col = cell_info
)
Applying MDS quickly reveals the underlying bifurcating topology of the dataset (from MEF to myocytes and neurons).
# compute distance matrix
dist <- dynutils::calculate_distance(dataset$expression, method = "pearson")
dim(dist)
## [1] 392 392
# compute MDS
dimred_mds <- cmdscale(dist)
# plot points
qplot(dimred_mds[,1], dimred_mds[,2], colour = dataset$grouping) +
theme_bw() +
labs(x = "Comp 1", y = "Comp 2", colour = "Group")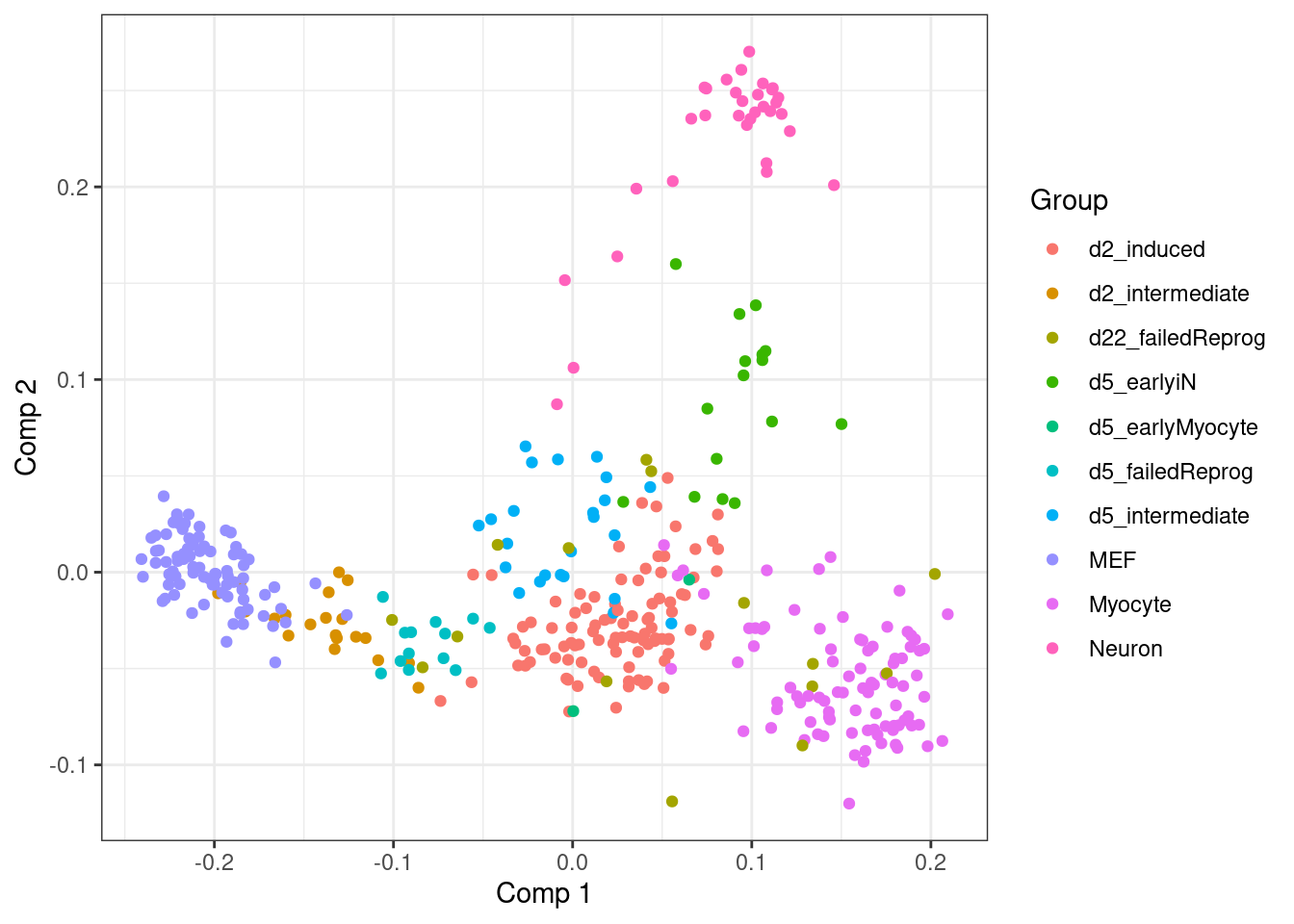
Regular MDS, however, requires computing all pairwise distances between data points. This dataset only contains 392 data points, but for datasets it is increasingly infeasible to apply MDS.
Landmark MDS
Landmark MDS (LMDS) (de Silva and Tenenbaum 2004) is an extension of MDS which scales much better with respect to the number of data points in the dataset. A short while ago, we published an R package on CRAN implementing this algorithm, lmds v0.1.0.
Landmark MDS only computes the distance matrix between a set of landmarks and all other data points. MDS is then only performed on the landmarks, and all other datapoints are projected into the landmark space.
library(lmds)
# compute distances between random landmarks and all data points
dist_landmarks <- select_landmarks(
dataset$expression,
distance_method = "pearson",
num_landmarks = 150
)
dim(dist_landmarks)
## [1] 150 392
# perform LMDS
dimred_lmds <- cmdscale_landmarks(dist_landmarks)
# plot points
qplot(dimred_lmds[,1], dimred_lmds[,2], colour = dataset$grouping) +
theme_bw() +
labs(x = "Comp 1", y = "Comp 2", colour = "Group")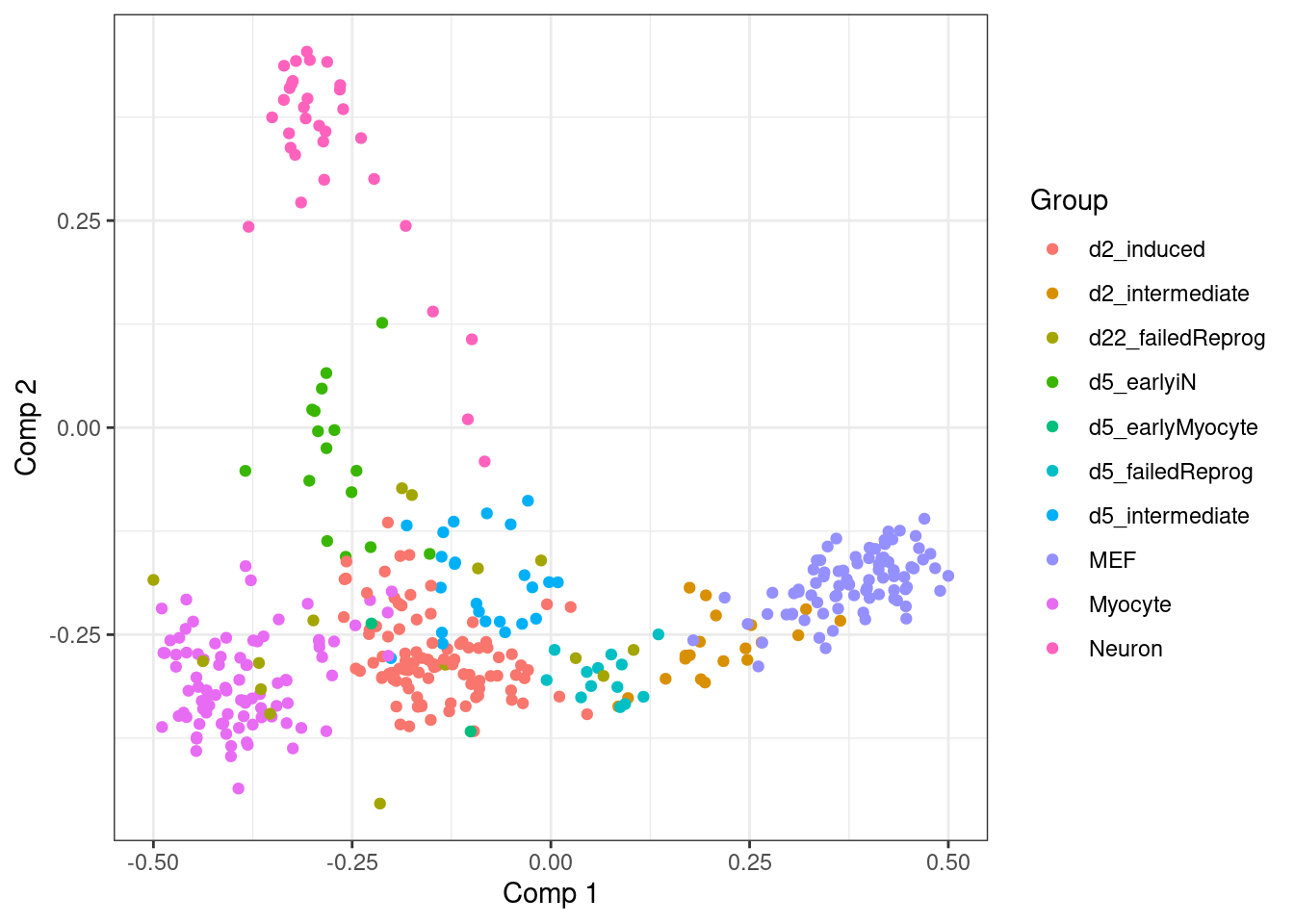
Most frequently, these two steps can be applied together as follows:
dimred_lmds2 <- lmds(
dataset$expression,
distance_method = "pearson",
num_landmarks = 150
)Execution time
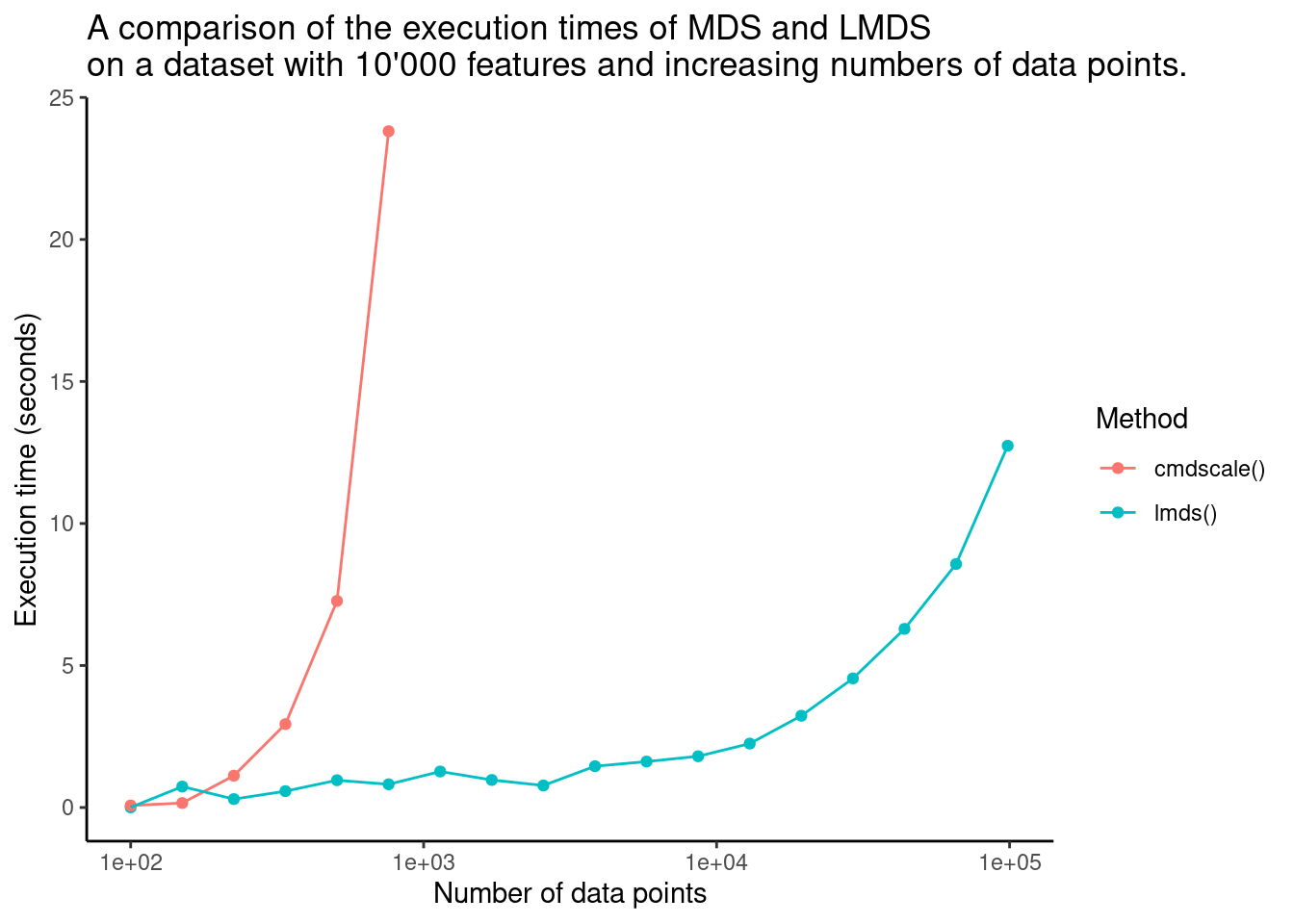
In the figure below, the execution times of MDS and LMDS are compared by increasing the size of a random dataset until the execution of either algorithms exceeds 10 seconds.
Conclusion
LMDS is a heuristic for MDS which scales linearly with respect to the number of points
in the dataset. Go ahead and check out our implementation for this algorithm,
available on CRAN.
If you encounter any issues, feel free to let me know by creating an
issue post on Github.
References
de Silva, Vin, and Joshua B Tenenbaum. 2004. “Sparse Multidimensional Scaling Using Landmark Points.” Technical Report, Stanford University, 41.
Kruskal, J. B. 1964. “Multidimensional Scaling by Optimizing Goodness of Fit to a Nonmetric Hypothesis.” Psychometrika 29 (1): 1–27. https://doi.org/10.1007/BF02289565.
Treutlein, Barbara, Qian Yi Lee, J Gray Camp, Moritz Mall, Winston Koh, Seyed Ali Mohammad Shariati, Sopheak Sim, et al. 2016. “Dissecting Direct Reprogramming from Fibroblast to Neuron Using Single-Cell RNA-Seq.” Nature 534 (7607): 391–95.